힙(Heap)의 동작방식과 시간복잡도를 설명해주세요

힙(Heap) 이란

우선순위 큐를 구현하기 위해 만들어진 완전 이진 트리형 자료구조

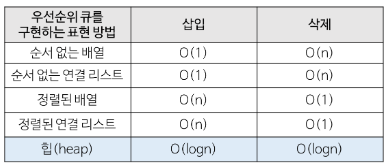
추가된 값들 중에서 최댓값이나 최솟값을 빠르게 찾을 수 있음
이진 탐색 트리와 달리 느슨한 반정렬 상태를 유지함
또한 중복된 값의 추가를 허용함
배열과 리스트에 비해 평균적으로 더 나은 효율을 보여줌

종류

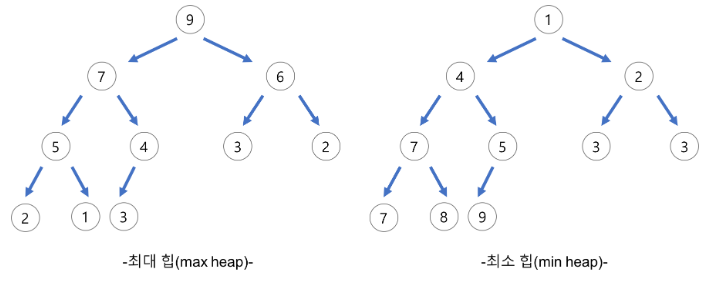
최소 힙 (부모노드 ≤ 자식노드 && 루트노드 == MAX)
최대 힙 (부모노드 ≥ 자식노드 && 루트노드 == MAX)

동작방식

1. 데이터의 추가

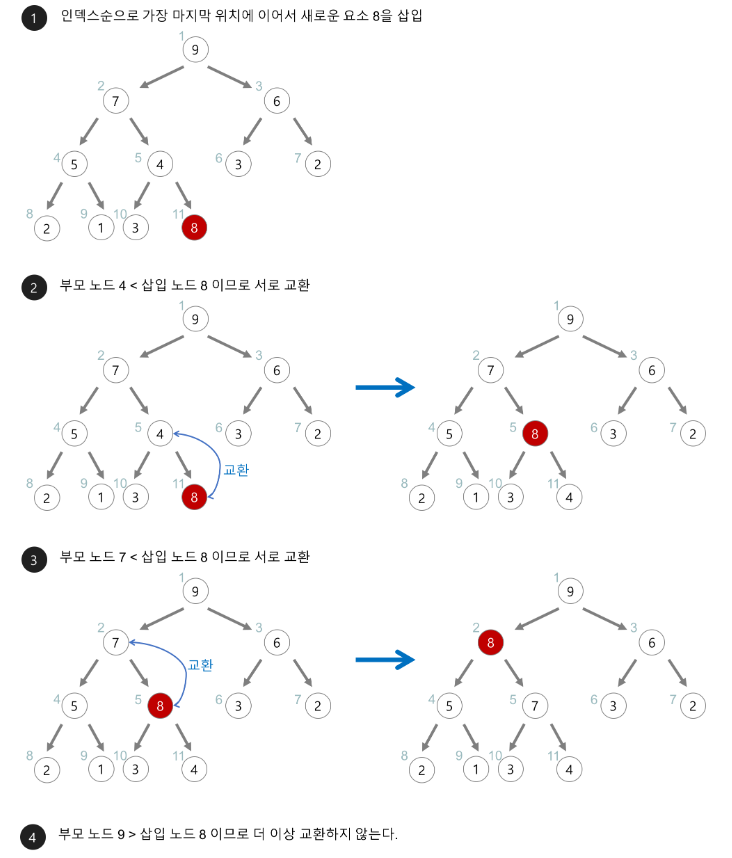
인덱스를 2로 나눈 값의 노드와 비교 (부모노드와 비교)
루트 노드까지 비교하는 경우, 시간 복잡도가 log(n)으로 최대이다.

데이터의 삭제

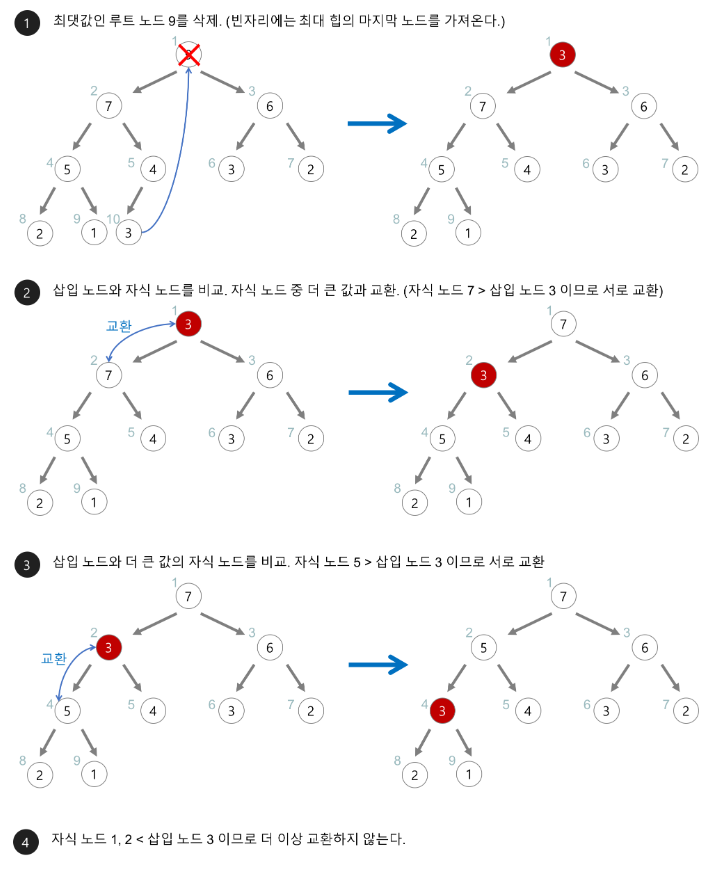
삭제 시 인덱스가 가장 높은 값이 루트노드를 대체
이후 자식 노드들과 비교하며 큰 값과 자리를 교환한다.
가장 아래까지 내려가는 경우 시간 복잡도가 log(n)으로 최대이다.
힙은 우선순위 큐를 토대로 한 자료구조이므로 중간값 삭제 및 추가는 고려하지 않는다.

추가) 구현방법

: 완전 이진 트리를 기반으로 하므로, 배열 상에서 구현이 가능하다.

JAVA로 구현한 코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


/* 최대힙 삽입 */
void insert_max_heap(int x){
	maxHeap[++heapSize] = x; // 힙 크기를 하나 증가하고 마지막 노드에 x를 넣는다.

	for (int i=heapSize; i>1; i/=2) {
	  // 마지막 노드가 자신의 부모 노드보다 크면 swap
	  if (maxHeap[i/2] < maxHeap[i]) {
	    swap(i/2, i);
	  } else {
	    break;
	  }
	}
}

/* 최대힙 삭제 */
int delete_max_heap(){
	if (heapSize == 0) // 배열이 빈 경우
	  return 0;

	int item = maxHeap[1]; // 루트 노드의 값을 저장한다.
	maxHeap[1] = maxHeap[heapSize]; // 마지막 노드의 값을 루트 노드에 둔다.
	maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드를 0으로 초기화한다.

	for (int i=1; i*2<=heapSize;) {
	  // 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 반복문을 나간다.
	  if (maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]) {
	    break;
	  }
	  // 왼쪽 노드가 더 큰 경우, 왼쪽 노드와 마지막 노드를 swap
	  else if (maxHeap[i*2] > maxHeap[i*2+1]) {
	    swap(i, i*2);
	    i = i*2;
	  }
	  // 오른쪽 노드가 더 큰 경우, 오른쪽 노드와 마지막 노드를 swap
	  else {
	    swap(i, i*2+1);
	    i = i*2+1;
	  }
	}
	return item;
	}
}